Graph Algorithms in Neo4j: Graph Algorithm Concepts

According to Frost & Sullivan, “Graphs are one of the unifying themes of computer science – an abstract representation that describes the organization of transportation systems, human interactions and telecommunication networks. That so many different structures can be modeled using a single formalism is a source of great power to the educated programmer.”

To tap this power, you need some basic concepts. This blog series is designed to help you better leverage graph analytics so you can effectively innovate and develop intelligent solutions faster.

Last week we looked at Neo4j graph analytics, and how a native graph platform is required to make it easy to express relationships across many types of data elements.

This week we examine graph algorithm concepts, including two fundamental graph traversal algorithms: breadth-first search (BFS) and depth- first search (DFS), and various graph properties that will inform your choice of how you traverse a graph and the algorithms you use.

Traversal

The most fundamental graph task is to visit nodes and relationships in a methodical way – this is called traversing a graph. Traversal means moving from one item to another using predecessor and successor operations in a sorted order.

Although this sounds simple, because the sorted order is logical, the next hop is determined by a node’s logical predecessor or successor and not by its physical nearness.

Complexity arises as values assigned to not only nodes but relationships may be factored in. For example, in an unsorted graph, a node’s predecessor would hold the largest value that is smaller than the current node’s value and its successor would be the node with the smallest value that is larger.

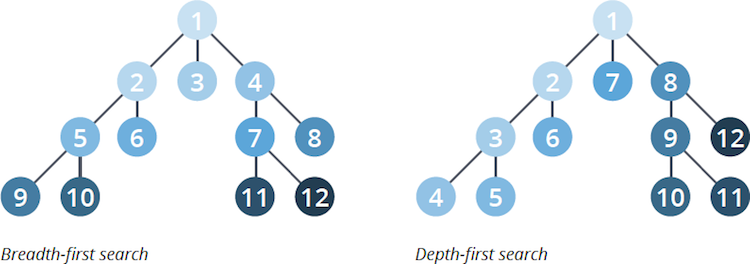
Fundamental Traversal Algorithms

There are two fundamental graph traversal algorithms: breadth-first search (BFS) and depth-first search (DFS).



The main difference between the algorithms is the order in which they explore nodes in the graph.

Breadth-first search traverses a graph by exploring a node’s neighbors first before considering neighbors of those neighbors. Depth-first search will explore as far down a path as possible, always visiting new neighbors where possible.

While they are not often used directly, these algorithms form an integral part of other graph algorithms:

• Depth-first search is used by the Strongly Connected Components algorithms.
• Breadth-first search is used by the Shortest Path, Closeness Centrality and Connected Components algorithms.

It’s sometimes not obvious which algorithm is being used by other graph algorithms. For example, Neo4j’s Shortest Path algorithm uses a fast bidirectional breadth-first search as long as any predicates can be evaluated while searching for the path.

Graph Properties

There are several basic properties of graphs that will inform your choice of how you traverse a graph and the algorithms you use.

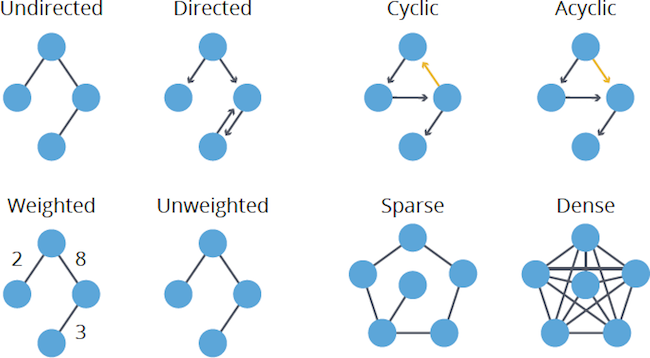
Undirected vs. Directed

In an undirected graph, there is no direction to the relationships between nodes. For example, highways between cities are traveled in both directions. In a directed graph, relationships have one specific direction. For example, within cities, some roads are one-way streets.

For some analyses, you may also want to ignore direction, like friendships where you want to assume the relationship is mutual. We’ll also see how this is relevant to Community Detection algorithms, especially Weakly and Strongly Connected Components.

Cyclic vs. Acyclic

In graph theory, cycles are paths through relationships and nodes where you walk from and back to a particular node.

There are many types of cycles within graphs, but cycles require consideration when using algorithms that may cause infinite loops, like PageRank, for example. An acyclic graph has no cycles; a tree structure is a common type of connected and acyclic (and undirected) graph.

Weighted vs. Unweighted

Weighted graphs assign values (weights) to either the nodes or their relationships; one example is the cost or time to travel a segment or the priority of a node.

The shortest path through an unweighted graph is quickly found with a breadth-first search as it will always be the path with the fewest number of relationships. Weighted graphs are commonly used in pathfinding algorithms and require consideration for calculating additional values.

Sparse vs. Dense

Graphs with a large number of relationships compared to nodes are called dense. Although not strictly defined, sparse graphs are loosely linear in the number of relationships to nodes, whereas in a clearly dense graph the number of relationships would typically be the square of the nodes. Most graphs tend toward sparseness, especially where physical elements, such as pipe sizes, come into play.

Care should be taken when preparing your graph data for community detection algorithms: On graphs that are extremely dense you’ll find overly clustered, meaningless communities; and at the other end of the spectrum, an extremely sparse graph may find no communities at all.

Conclusion

As we’ve seen, there are several basic properties of graphs that will inform your choice of how you traverse a graph and the algorithms that you will use.

Next week, we will take a look at the Neo4j Graph Algorithms Library. We developed the library as part of our effort to make it easier to use Neo4j for a wider variety of applications.

In the coming weeks, we’ll take an in-depth look at pathfinding and graph search algorithms.