Graph Algorithms in Neo4j: Strongly Connected Components

Graph algorithms provide the means to understand, model and predict complicated dynamics such as the flow of resources or information, the pathways through which contagions or network failures spread, and the influences on and resiliency of groups.

This blog series is designed to help you better utilize graph analytics and graph algorithms so you can effectively innovate and develop intelligent solutions faster using a graph database like Neo4j.

Last week we wrapped up our look at Centrality algorithms, with our look at the Closeness Centrality algorithm.



This week we begin our exploration of Community Detection algorithms, with a look at the Strongly Connected Components algorithm, which locates groups of nodes where each node is reachable from every other node in the same group, following the direction of relationships. It’s often applied from a depth-first search.

About Strongly Connected Components

The Strongly Connected Components (SCC) algorithm finds sets of connected nodes in a directed graph, where each node is reachable in both directions from any other node in the same set. It is often used early in a graph analysis process to give us an idea of how our graph is structured.

SCC is one of the earliest graph algorithms, and the first linear-time algorithm was described by Tarjan in 1972. Decomposing a directed graph into its strongly connected components is a classic application of the depth-first search algorithm.

When Should I Use Strongly Connected Components?

• In the analysis of powerful transnational corporations, SCC is used to find the set of firms in which every member directly owns and/or indirectly owns shares in every other member. Although it has benefits, such as reducing transaction costs and increasing trust, this type of structure weakens market competition. Read more in “The Network of Global Corporate Control.”
• SCC has been used to compute the connectivity of different network configurations when measuring routing performance in multihop wireless networks. Read more in “Routing performance in the presence of unidirectional links in multihop wireless networks.”
• Strongly Connected Components algorithms are often used as a first step in many graph algorithms that work only on strongly connected graphs. In social networks, a group of people is generally strongly connected (for example, students of a class or any other common place). Many people in these groups generally like some common pages or play common games. The SCC algorithms are used to find such groups and suggest the commonly liked pages or games to the people in the group who have not yet liked those pages or games.

Strongly Connected Components Example

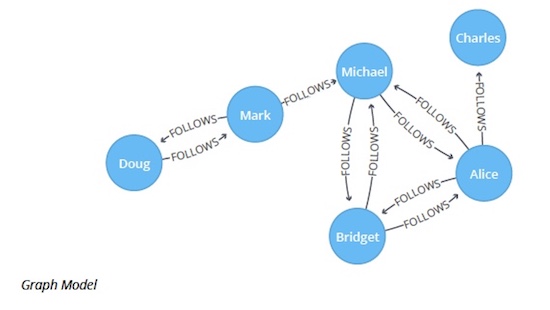
Let’s see the Strongly Connected Components algorithm in action. The following Cypher statement creates a Twitter-esque graph containing users and FOLLOWS relationships between them.

MERGE (nAlice:User {id:"Alice"})
MERGE (nBridget:User {id:"Bridget"})
MERGE (nCharles:User {id:"Charles"})
MERGE (nDoug:User {id:"Doug"})
MERGE (nMark:User {id:"Mark"})
MERGE (nMichael:User {id:"Michael"})
MERGE (nAlice)-[:FOLLOWS]->(nBridget)
MERGE (nAlice)-[:FOLLOWS]->(nCharles)
MERGE (nMark)-[:FOLLOWS]->(nDoug)
MERGE (nMark)-[:FOLLOWS]->(nMichael)
MERGE (nBridget)-[:FOLLOWS]->(nMichael)
MERGE (nDoug)-[:FOLLOWS]->(nMark)
MERGE (nMichael)-[:FOLLOWS]->(nAlice)
MERGE (nAlice)-[:FOLLOWS]->(nMichael)
MERGE (nBridget)-[:FOLLOWS]->(nAlice)
MERGE (nMichael)-[:FOLLOWS]->(nBridget);

Now we can run Strongly Connected Components to see whether everybody is connected to each other. Execute the following query:

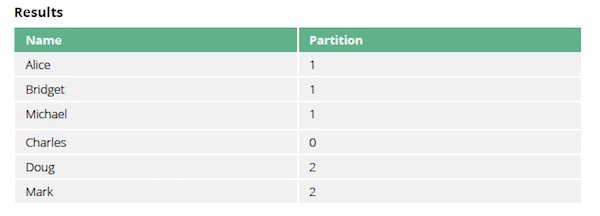
CALL algo.scc.stream("User","FOLLOWS")
YIELD nodeId, partition
MATCH (u:User) WHERE id(u) = nodeId
RETURN u.id AS name, partition

Visualization of Strongly Connected Components

We have three strongly connected components in our sample graph.

The first, and biggest, component has members Alice, Bridget and Michael, while the second component has Doug and Mark. Charles ends up in his own component because there isn’t an outgoing relationship from that node to any of the others.

Conclusion

As we’ve seen, the Strongly Connected Components algorithm is often used to enable running other algorithms independently on an identified cluster. As a preprocessing step for directed graphs, it helps quickly identify disconnected groups.

Next week we’ll continue our focus on Community Detection algorithms, with a look at Weakly Connected Components.