Unlocking DAGs in Neo4j: From Basics to Critical Path Analysis

During the recent NODES 2023 conference, Neo4j introduced several enhancements, including the addition of two DAG algorithms to their Graph Data Science library: Longest Path and Topological Sort. As the application of Directed Acyclic Graphs (DAGs) becomes increasingly relevant in diverse fields, it’s an opportune moment to delve into their practicality. In this article, we’ll explore the essence of DAGs, their applications, and demonstrate their potential through an in-depth analysis of a Gantt chart’s critical path. Let’s begin. DAG algorithms – Neo4j Graph Data Science

What is a DAG?

A DAG stands for Directed Acyclic Graph. Breaking that down:

• “Directed” means that connections (edges) between points (vertices) have a direction — they point from one vertex to another.
• “Acyclic” means that it doesn’t contain any cycles. In other words, if you start at any vertex v and begin walking along the directed edges, you’ll never loop back to v again.

Imagine a DAG as space-time. You might have some latitude in deciding where to go, whether it’s a visit to Hawaii or dancing the Polska. However, just like time, the direction in a DAG is non-negotiable; it’s a one-way journey. Unless you possess a plutonium-boosted DeLorean — but that’s a topic for another day!

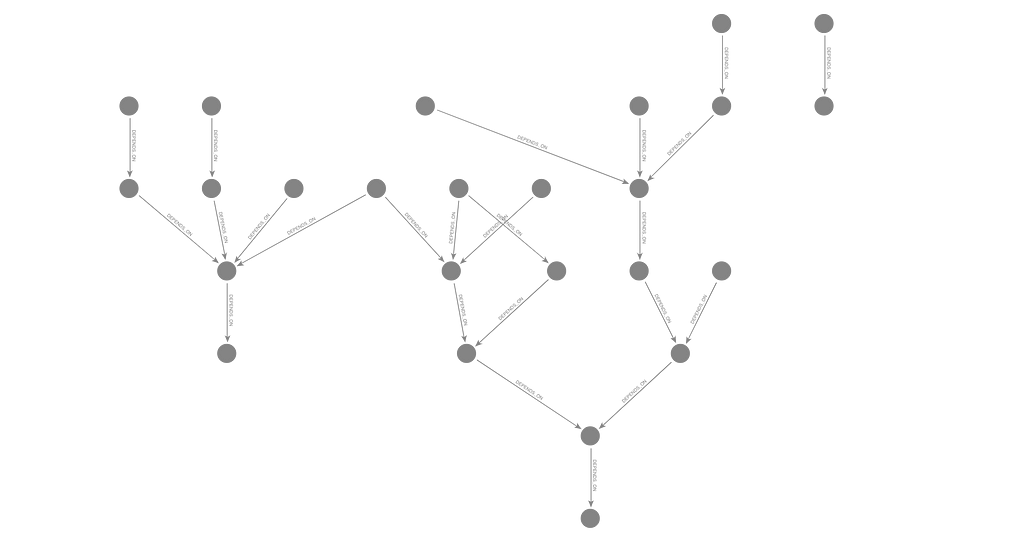
Why are DAGs useful?

Now that you’re familiar with Directed Acyclic Graphs (DAGs), you might be wondering, “What practical applications do they have?” Well, DAGs are not just theoretical constructs but serve as the backbone for various real-world applications.

1. Supply Chain Management: Whether tracking raw materials to finished products or overseeing the various steps involved in producing a product, DAGs are crucial. They ensure there are no cyclic dependencies, which could lead to inefficiencies or breakdowns in the supply chain.
2. Project Management & Scheduling: Ever heard of the critical path method in project scheduling? That’s DAGs at work! They help determine the shortest time a project can be completed by highlighting dependencies between tasks.
3. Causal Structures: In many scientific studies, it’s essential to understand cause and effect without cyclic redundancy. DAGs provide a clear representation of such relationships.
4. Citation Graphs: Academic papers often cite previous works. By visualizing these citations as a DAG, one can track the lineage of knowledge and identify foundational papers.
5. Microprocessors: In computer architecture, especially when optimizing instruction pipelining, DAGs help ensure a non-cyclic flow of operations.
6. Dependency Management: Dependencies form DAGs, be it in Software or Services. Determining what you depend on and how it influences your project can be critical, especially from a security perspective.

… and the list goes on.

One particularly interesting application I’ll delve into further is the use of DAGs in Gantt diagrams to identify critical paths, especially at scale. This method provides a clear overview of task dependencies and durations, pinpointing potential bottlenecks. Ready to see it in action?

Critical Path Analysis: DAGs & Gantt Diagrams

In the realm of project management, the Gantt chart stands as a pivotal tool. It’s a visual representation of a project’s timeline, showcasing when each task begins, its duration, and when it concludes. Gantt charts offer a clear view of task dependencies, allowing managers to determine which activities rely on the completion of others. Within this framework lies the concept of the critical path. It represents the longest sequence of tasks in a project that must be completed on time for the entire project to stay on schedule. In essence, any delay in the tasks on the critical path would directly impact the project’s end date. Critical Path Analysis (CPA) takes this a step further. It’s a technique used to identify these crucial tasks, determining the shortest time in which a project can be completed. By focusing on these pivotal tasks, project managers can allocate resources more efficiently and address potential bottlenecks proactively. Understanding these concepts becomes essential when aiming for timely project completion without unforeseen delays.

From Simple to Scalable

Wikipedia’s Gantt Chart: A Starting Point

Let’s commence with a recognizable example. If you’ve ever browsed the Wikipedia article on Gantt charts, you’ll recall a straightforward project timeline. We’ll ingest this example into Neo4j, representing it as a dependency DAG.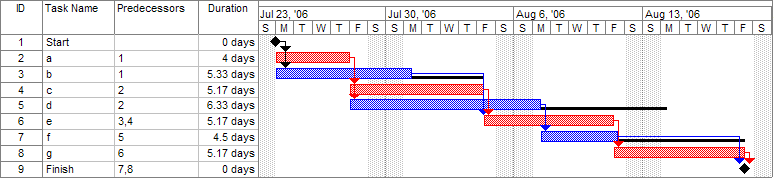

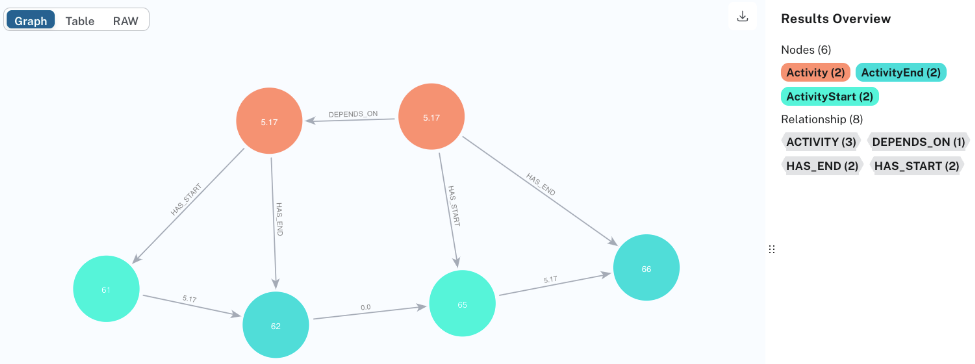
Before diving into the analysis, there’s a pivotal step: refactoring our graph to suit the algorithm’s requirements. Initially, our model looks like this: (:Activity)-[:DEPENDS_ON]->(:Activity). However, the gds.dag.longestPath algorithm leverages edge weights, necessitating a slight modification. To accommodate this, we’ll invert our graph. Each Activity node will be split into two nodes: (ActivityStart) and (ActivityEnd), connected by an edge [:ACTIVITY {expectedTime: <expected time>}]. Dependencies, on the other hand, will be represented as edges stemming from (ActivityEnd) to (ActivityStart), with an expectedTime of 0.0, signaling no time lapse between the two.

With our data restructured, we’re primed to employ Neo4j’s gds.dag.longestPath algorithm to determine the critical path. This path highlights the sequence of tasks that, if delayed, would prolong the entire project. While that would be overkill if you’re just interested in a single path with a few nodes, if you have a large graph and want to serve the longest paths from arbitrary starting points concurrently, it makes sense to create an optimized structure. We start by projecting the relevant path into the in-memory compute representation.

With our critical path identified, it’s not just about pinpointing the longest-duration tasks. A comprehensive project plan requires a detailed schedule for each task. Leveraging the insights from our critical path analysis, we can determine start and end times for all tasks, ensuring dependencies are respected and resources optimally allocated. This approach provides a clear roadmap for the entire project, allowing managers not only to foresee potential bottlenecks but also to adapt and adjust as the project evolves. While this example is illustrative, real-world scenarios often comprise far more complex projects with thousands of tasks and dependencies. Can our approach still hold water?

Scaling It Up: A Massive DAG

To address this, we’ve crafted a synthetic dataset: a sprawling DAG with 10,000 tasks and around a whopping 5 million dependencies. The objective remains unchanged: identify the critical path and facilitate efficient project planning. Applying the same refactoring andgds.dag.longestPath algorithm, we can swiftly pinpoint the critical path even in this colossal dataset, showcasing the scalability of our approach.

The full schedule is computed on a regular laptop in less than 3 seconds.

activity,dependencies,expected_time,planned_start,planned_end
0,[],9.32,0.0,9.32
1,[],2.37,0.0,2.37
2,[],5.94,0.0,5.94
3,[],3.81,0.0,3.81
4,[0],2.06,9.32,11.38
...
4999,"[446, 4978, 4990, 4942, 4933, 4957, 4925, 4948, 4980, 4962, 4998, 4985, 4943, 4935, 4950, 4907, 4877, 4888, 4893, 4857, 4852, 4836, 4839, 4807, 4808, 4799, 4778, 4811, 4776, 4772, 4743, 4745, 4731, 4708, 4684, 4691, 4700, 4670, 4648, 4594, 4606, 4589, 4579, 4577, 4565, 4563, 4510, 4502, 4505, 4488, 4469, 4466, 4449, 4434, 4432, 4399, 4403, 4404, 4400, 4407, 4384, 4377, 4378, 4375, 4363, 4373, 4350, 4359, 4334, 4339, 4325, 4321, 4320, 4319, 4309, 4284, 4285, 4270, 4263, 4233, 4240, 4214, 4210, 4211, 4193, 4164, 4171, 4153, 4141, 4133, 4110, 4100, 4097, 4091, 4094, 4078, 4086, 4074, 4061, 4063, 4039, 4043, 4028, 4033, 4002, 3970, 3979, 3961, 3965, 3967, 3968, 3952, 3951, 3924, 3909, 3897, 3892, 3886, 3888, 3891, 3873, 3880, 3859, 3824, 3814, 3801, 3802, 3783, 3758, 3763, 3753, 3745, 3736, 3744, 3718, 3722, 3723, 3720, 3706, 3711, 3707, 3680, 3671, 3659, 3651, 3645, 3638, 3616, 3613, 3603, 3604, 3583, 3576, 3572, 3555, 3541, 3533, 3517, 3516, 3502, 3498, 3483, 3484, 3462, 3464, 3454, 3446, 3451, 3429, 3394, 3365, 3373, 3331, 3326, 3319, 3311, 3315, 3280, 3259, 3246, 3236, 3215, 3190, 3179, 3176, 3175, 3168, 3162, 3159, 3151, 3157, 3137, 3126, 3122, 3113, 3117, 3103, 3101, 3072, 3070, 3066, 3048, 3057, 3055, 3052, 3040, 3033, 3030, 3022, 3019, 3028, 3001, 2992, 2995, 2981, 2982, 2961, 2966, 2955, 2954, 2922, 2913, 2917, 2920, 2892, 2894, 2895, 2885, 2876, 2871, 2860, 2844, 2839, 2819, 2802, 2786, 2783, 2737, 2739, 2719, 2725, 2689, 2682, 2671, 2654, 2649, 2640, 2625, 2627, 2612, 2615, 2589, 2568, 2553, 2554, 2557, 2521, 2526, 2518, 2516, 2510, 2509, 2499, 2491, 2475, 2467, 2458, 2455, 2450, 2443, 2433, 2424, 2430, 2427, 2406, 2413, 2411, 2389, 2346, 2347, 2336, 2335, 2316, 2319, 2308, 2297, 2305, 2288, 2285, 2286, 2276, 2261, 2264, 2224, 2211, 2206, 2200, 2201, 2193, 2157, 2134, 2136, 2119, 2111, 2112, 2118, 2095, 2063, 2068, 2056, 2041, 2029, 2012, 2015, 1999, 2001, 2006, 1998, 1993, 1983, 1895, 1884, 1880, 1871, 1863, 1866, 1849, 1840, 1837, 1797, 1798, 1801, 1786, 1782, 1772, 1753, 1715, 1701, 1686, 1694, 1648, 1637, 1621, 1579, 1576, 1566, 1563, 1549, 1542, 1544, 1527, 1528, 1519, 1507, 1497, 1491, 1484, 1479, 1461, 1458, 1459, 1432, 1428, 1408, 1411, 1404, 1401, 1354, 1356, 1313, 1301, 1274, 1272, 1264, 1234, 1223, 1225, 1210, 1203, 1200, 1178, 1161, 1144, 1133, 1138, 1115, 1086, 1073, 1049, 999, 1003, 976, 947, 952, 914, 909, 901, 900, 884, 841, 846, 838, 839, 832, 816, 795, 785, 774, 771, 766, 753, 754, 737, 730, 707, 701, 690, 692, 676, 670, 637, 635, 634, 621, 622, 607, 590, 592, 578, 568, 569, 547, 542, 511, 515, 503, 492, 477, 473, 450, 57, 50, 78, 79, 101, 116, 115, 113, 120, 122, 123, 130, 131, 151, 172, 166, 169, 190, 186, 200, 213, 217, 226, 246, 248, 261, 257, 273, 264, 276, 275, 285, 302, 303, 327, 325, 342, 354, 375, 385, 396, 399, 392, 393, 401, 415, 420, 439, 435, 448]",4.12,4616.269999999992,4620.389999999992

GDS vs. Cypher-only Longest Path: A benchmark

To truly appreciate the efficiency of the LongestPath algorithm, let’s set up a benchmark comparison. We’ll evaluate the performance of the GDS algorithm against an equivalent Cypher query. This will provide a concrete understanding of the advantages and capabilities offered by Neo4j’s specialized algorithms in handling complex graph operations. Now, let’s dive into the specifics. Below is the Cypher query we’ll be using for this benchmark. This query has been crafted to mirror the functionality of the GDS algorithm, allowing for a direct comparison of their performances in a similar operational context.

MATCH p=(a)-[r:ACTIVITY]->*(b:ActivityEnd)
WITH b.name AS name,
     reduce(total_time = 0, act IN r |
        total_time + act.expected_time) AS total_time
RETURN name, max(total_time) AS longest_time

Take a moment to examine the query. Notice its structure and how it’s designed to accomplish the task at hand. Next, we will run this query against our dataset and record its performance metrics, which will then be compared to the GDS algorithm’s. As part of our comprehensive benchmarking, we’ll test across several datasets, each escalating in size and complexity. The datasets will vary in the number of tasks they contain, but all will maintain a constant 5% probability of a dependency existing between any two tasks. This approach ensures we are not just testing performance in a single scenario, but assessing how the Cypher query and the GDS algorithm scale with increasing data volumes and complexity.

The benchmark results clearly showcase the GDS algorithm’s superior performance and scalability over Cypher queries in this use case. In smaller graphs, GDS significantly outperforms Cypher (15ms vs. 2727ms). This efficiency gap becomes even more pronounced in larger datasets. For instance, with 50K dependencies, GDS completes the task in just 51ms, whereas Cypher fails to complete it at all. This trend continues with the largest tested dataset (1M+ dependencies), where GDS remains efficient (696ms), while Cypher fails to yield results again. In essence, these findings underline the critical advantage of using Neo4j’s GDS algorithms for handling extensive and complex graph data, emphasizing their robustness and efficiency in managing high volumes of relationships. The results are clear. Whether you’re dealing with a straightforward project or a mammoth endeavor, Neo4j, coupled with critical path analysis, ensures you’re always ahead of the curve, ready to tackle challenges head-on.

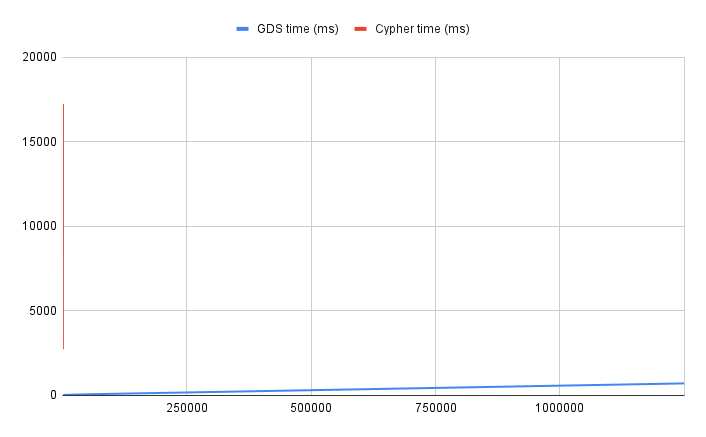
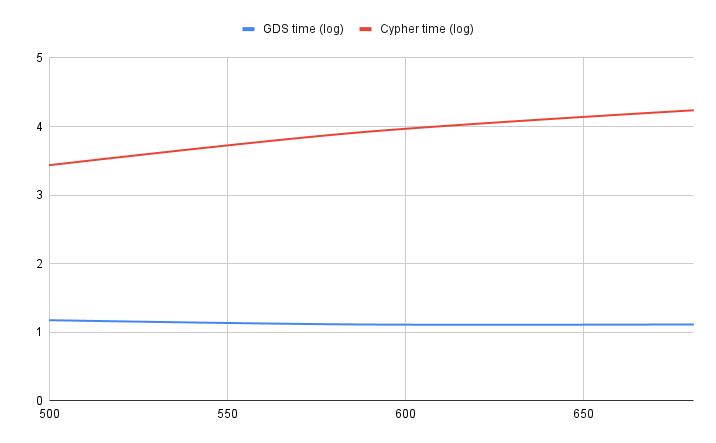
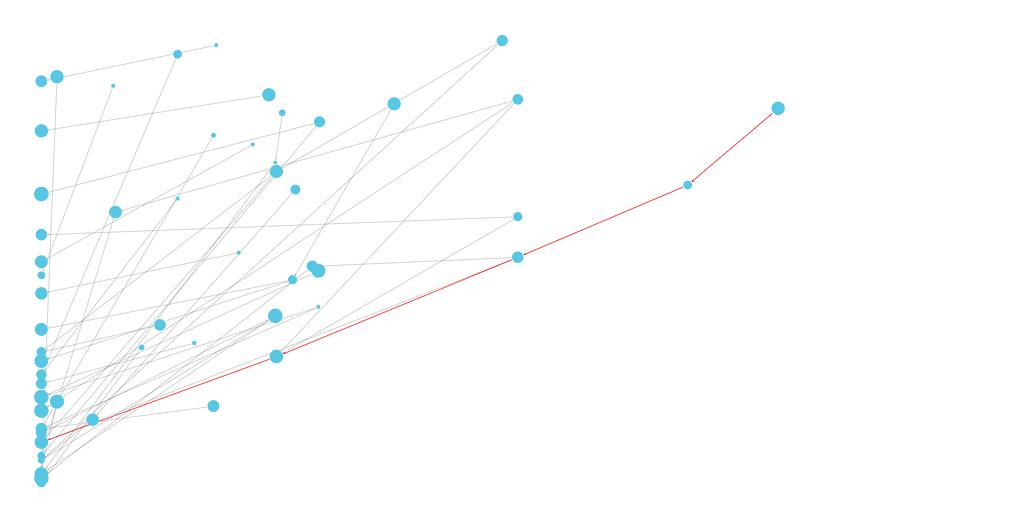
Conclusion

In the vast landscape of graph analytics, Neo4j continues to pioneer tools and techniques that drive business success. While Directed Acyclic Graphs (DAGs) offer powerful insights, particularly in project optimization and management, they represent just a facet of what graphs can achieve. As we’ve explored through Gantt chart analysis and beyond, the true potential lies in a holistic approach. Neo4j’s diverse offerings enable businesses to tap into a myriad of insights, fostering innovation, informed decision-making, and strategic growth. Check out the other presentations from NODES 2023 for 100 more impressive graph talks:

---

Unlocking DAGs in Neo4j: From Basics to Critical Path Analysis was originally published in Neo4j Developer Blog on Medium, where people are continuing the conversation by highlighting and responding to this story.