Exploring Fraud Detection With Neo4j & Graph Data Science – Part 2

Data Science Product Specialist, Neo4j
6 min read
Identifying communities that reflect underlying groups of individuals is often a key step to fraud detection. In part 1 of this series, we explored with Louvain. In part 2, we will provide more formal definitions for resolving entities that will allow us to partition well-defined communities in a scalable manner.
To accomplish this, we will define some Entity Resolution (ER) rules that will allow us to draw relationships between users we believe belong to the same underlying community.
We will then use the Weakly Connected Components (WCC) algorithm to resolve the communities. And lastly, we will label all users in communities that include flagged accounts as fraud risks.
The technical resources to reproduce this analysis and the analysis in all other parts of this series are contained in this GitHub repository, which includes an iPython notebook and link to the dataset.
Entity Resolution (ER) Business Rules
We will now apply Entity Resolution (ER) to resolve groups of individuals behind sets of user accounts. For this analysis, we will use some pretty straightforward ER business logic. If either of the two below conditions are true, we will resolve two user accounts by linking them together with a new relationship type.
- One user sent money to another user that shares the same credit card
- Two users share a card or device connected to less than or equal to 10 total accounts, and those two users also share at least two other identifiers of type credit card, device, or IP address
You could switch out or add different rules to the above — these are just examples. In a real-world scenario these business rules would pass by SMEs and possibly be backed by further supervised machine learning on manually labeled data. More advanced techniques for this type of ER are possible in graph, and we describe them in this white paper and this blog.
For a P2P dataset, we do not necessarily want to label all senders/receivers of flagged user transactions as fraudulent, since some fraud schemes involve transactions with victims. Furthermore, additional identifiers such as IP may be inexact and cards + devices can be fraudulently controlled/used without the owner’s permission. Hence I used somewhat stringent rules that aligned with the patterns noted in part 1. We can apply the ER relationships with Cypher:
# P2P with shared card rule
gds.run_cypher('''
MATCH (u1:User)-[r:P2P]->(u2)
WITH u1, u2, count(r) AS cnt
MATCH (u1)-[:HAS_CC]->(n)<-[:HAS_CC]-(u2)
WITH u1, u2, count(DISTINCT n) AS cnt
MERGE(u1)-[s:P2P_WITH_SHARED_CARD]->(u2)
RETURN count(DISTINCT s) AS cnt
''')
cnt
6240
# shared ids rule
gds.run_cypher('''
MATCH (u1:User)-[:HAS_CC|USED]->(n)<-[:HAS_CC|USED]-(u2)
WHERE n.degree <= 10 AND id(u1) < id(u2)
WITH u1, u2, count(DISTINCT n) as cnt
MATCH (u1)-[:HAS_CC|USED|HAS_IP]->(m)<-[:HAS_CC|USED|HAS_IP]-(u2)
WITH u1, u2, count(DISTINCT m) as cnt
WHERE cnt > 2
MERGE(u1)-[s:SHARED_IDS]->(u2)
RETURN count(DISTINCT s)
''')
count(DISTINCT s)
5316
Using Weakly Connected Components (WCC) to Resolve Communities
Weakly Connected Components (WCC) is a practical and highly scalable community detection algorithm. It is also deterministic and very explainable. It defines a community simply as a set of nodes connected by a subset of relationship types in the graph. This makes WCC a good choice for formal community assignment in production fraud detection settings.
Below we run WCC on users via the ER relationships created above:
g, _ = gds.graph.project('comm-projection', ['User'], {
'SHARED_IDS': {'orientation': 'UNDIRECTED'},
'P2P_WITH_SHARED_CARD': {'orientation': 'UNDIRECTED'}
})
df = gds.wcc.write(g, writeProperty='wccId')
g.drop()
df
writeMillis
79
nodePropertiesWritten
33732
componentCount
28203
componentDistribution
{'p99': 3, 'min': 1, 'max': 175, 'mean': 1.196042974151686, 'p90': 2, 'p50': 1, 'p999': 8, 'p95': 2, 'p75': 1}
postProcessingMillis
13
preProcessingMillis
0
computeMillis
11
configuration
{'writeConcurrency': 4, 'seedProperty': None, 'consecutiveIds': False, 'writeProperty': 'wccId', 'threshold': 0.0, 'relationshipWeightProperty': None, 'nodeLabels': ['*'], 'sudo': False, 'relationshipTypes': ['*'], 'username': None, 'concurrency': 4}
2,8203 components were created. The majority of the components are of size 1 representing a component with just a single user, not resolved to any other. The max component size is 175 users, which means the largest community has 175 users.
Labeling Fraud Risk User Accounts
As these communities are meant to label underlying groups of individuals, if even one flagged account is in the community, we will label all user accounts in the group as fraud risks:
gds.run_cypher('''
MATCH (f:FlaggedUser)
WITH collect(DISTINCT f.wccId) AS flaggedCommunities
MATCH(u:User) WHERE u.wccId IN flaggedCommunities
SET u:FraudRiskUser
SET u.fraudRisk=1
RETURN count(u)
''')
count(u)
452
This gives us a total of 452 fraud risk accounts which means if we subtract the 241 already flagged accounts we identified 211 new fraud risk user accounts.
WCC Community Statistics
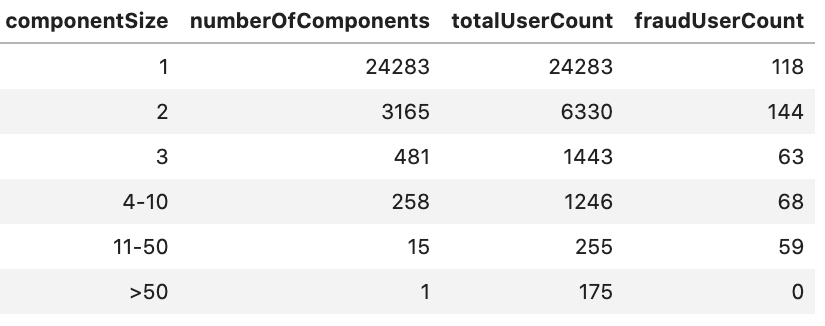
The breakdown of communities by size is listed below. The majority are single user communities. Only a small portion have multiple users and of those, community sizes are mostly 2 and 3. Larger communities are rare. However, if we look at the fraudUser accounts we will see that the majority reside in multi-user communities. The 118 fraud accounts in single user communities are flagged users (via original chargeback logic) that have yet to be resolved to a community.
gds.run_cypher( '''
MATCH (u:User)
WITH u.wccId AS community, count(u) AS cSize, sum(u.fraudRisk) AS cFraudSize
WITH community, cSize, cFraudSize,
CASE
WHEN cSize=1 THEN ' 1'
WHEN cSize=2 THEN ' 2'
WHEN cSize=3 THEN ' 3'
WHEN cSize>3 AND cSize<=10 THEN ' 4-10'
WHEN cSize>10 AND cSize<=50 THEN '11-50'
WHEN cSize>10 THEN '>50' END AS componentSize
RETURN componentSize,
count(*) AS numberOfComponents,
sum(cSize) AS totalUserCount,
sum(cFraudSize) AS fraudUserCount
ORDER BY componentSize
''')
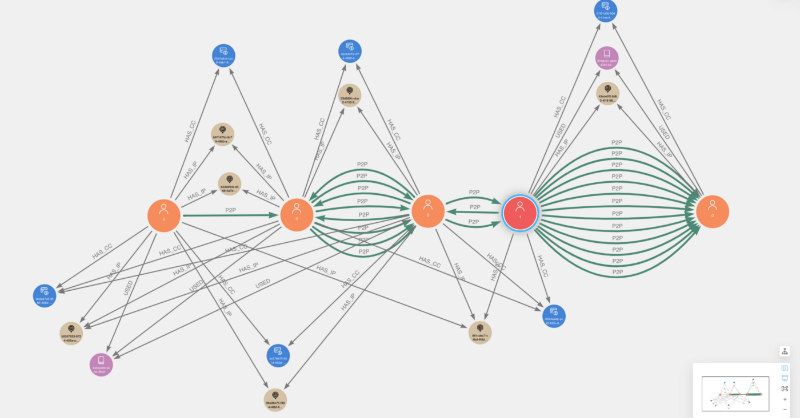
Below are a couple examples of the fraud communities visualized in Neo4j Bloom. Users that were flagged via initial chargeback logic are colored red with caption=1, while other users are colored orange with caption=0. Overall, you will notice a high degree of overlapping connectivity of identifiers and P2P transactions between users, which we should expect given our ER rules.
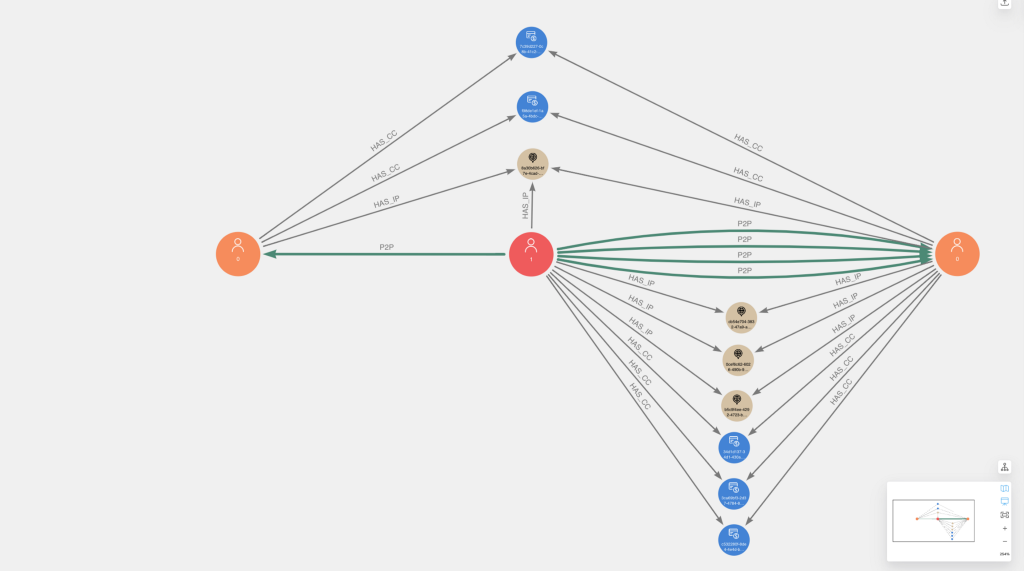
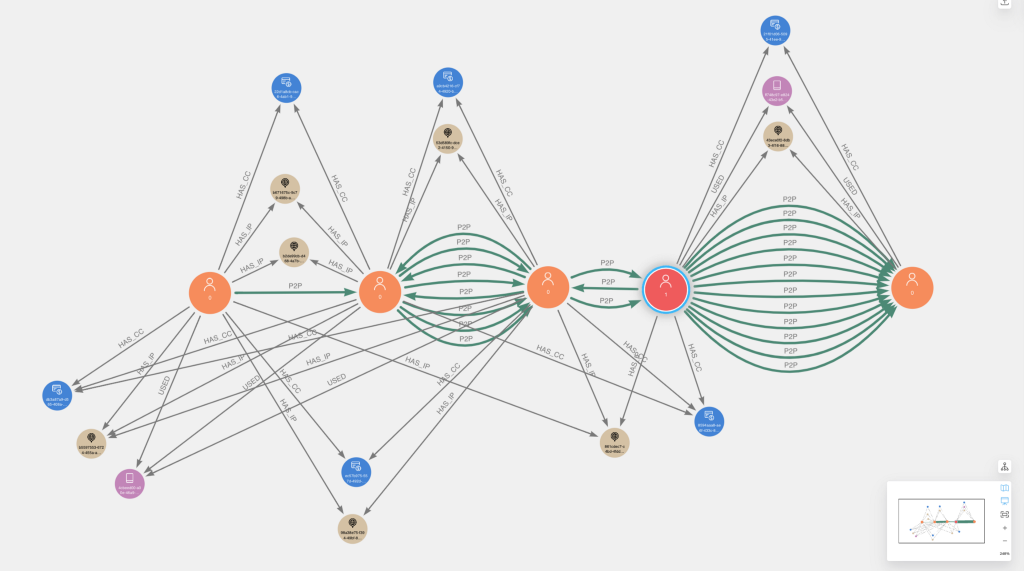
Outcomes of Fraud Risk Labeling
Fraud Risk labeling helped identify an additional 211 new fraud risk user accounts, nearly doubling the number of known fraud users (87.5 percent increase). We also see that 65 percent of the money going to/from previously flagged accounts and other users can be attributed to the newly identified risk accounts:
gds.run_cypher('''
MATCH (:FlaggedUser)-[r:P2P]-(u) WHERE NOT u:FlaggedUser
WITH toFloat(sum(r.totalAmount)) AS p2pTotal
MATCH (u:FraudRiskUser)-[r:P2P]-(:FlaggedUser) WHERE NOT u:FlaggedUser
WITH p2pTotal, toFloat(sum(r.totalAmount)) AS fraudRiskP2pTotal
RETURN round((fraudRiskP2pTotal)/p2pTotal,3) AS p
''').p[0]
0.652
Additionally, while the newly identified 211 accounts represents less than 1 percent of total users in the sample, 12.7 percent of the total P2P amount in the sample involved the newly identified accounts as senders or receivers:
gds.run_cypher('''
MATCH (:User)-[r:P2P]->()
WITH toFloat(sum(r.totalAmount)) AS p2pTotal
MATCH (u:FraudRiskUser)-[r:P2P]-() WHERE NOT u:FlaggedUser
WITH p2pTotal, toFloat(sum(r.totalAmount)) AS fraudRiskP2pTotal
RETURN round((fraudRiskP2pTotal)/p2pTotal,3) AS p
''').p[0]
0.127
Finally, we can see an improvement in card and device discrimination with many more cards and devices being used by fraud risk accounts exclusively.
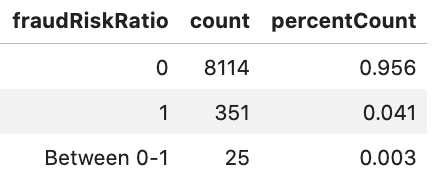
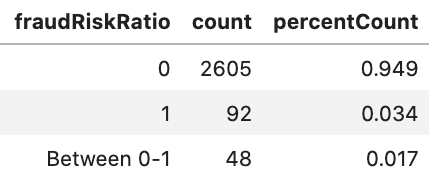
The aggregate P2P statistics combined with improvements in Card and Device metrics are significant given the limited scope of the previously flagged fraud, which focused on chargebacks. These results strongly imply that there are more sophisticated networks of fraudulent money flows behind the chargebacks, rather than the chargebacks being isolated occurrences.
In the next part of this series, we will cover how to use other graph algorithms to triage even more suspicious accounts and community patterns in the graph.
Here’s your key to the whole series: