Tic Tac Toe Challenge in Cypher

Director of Engineering, Neo4j
19 min read

We will look at how to use Cypher, the query language for the Neo4j graph database, to write a computer player for a five-in-a-row game, and a competition we had with this for the colleagues at Neo4j.
“A strange game. The only winning move is not to play. How about a nice game of chess?”
– A quote from the movie War Games (1983) just after they have shown the intelligent (?) computer that thermonuclear war, just like Tic Tac Toe, is a game with no winners.

But unlike nuclear war you can make Tic Tac Toe more interesting by expanding the 3*3 board to a much larger grid and making it a five-in-a-row.
It is also a game for which you can write computer players without necessarily exploring advanced AI algorithms. And, just like everything else in the world, the game board of Tic Tac Toe is a graph.
This all made it ideal for a competition for my colleagues at Neo4j. How good are we at writing winning Cypher queries?
The Game
For the contest, I wrote a simple five-in-a-row game in Java, with a configurable grid size, a simple user interface, and the game state held in a Neo4j database.

The challenge for the participants was to come up with one single Cypher query that makes one move for a player. Then, we had a tournament where the players were pitched against each other.
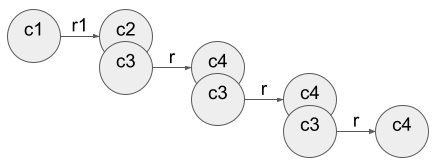
The data model used in the database for the game state was a very simple one with only one node type and one relationship type:

So the graph for a 3*3 game board (which wouldn’t make much sense for a five in a row, but just for illustration purposes) would look like this:
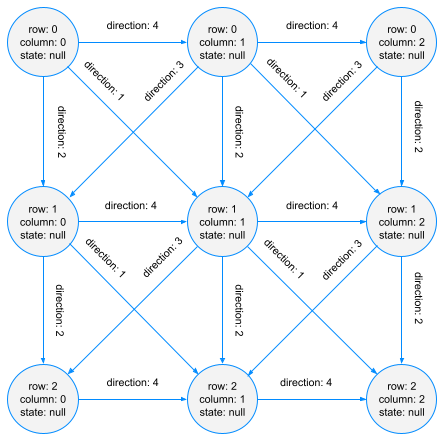
The Cypher queries had three parameters they could use
- $symbol: The symbol, either “X” or “O”, of this player
- $width: The width of the game board (# of cells)
- $height: The height of the game board (# of cells)
So the simplest possible query (which would just put the mark in the first cell found) would look like this:
MATCH (c:Cell)
WHERE c.state IS NULL
WITH c LIMIT 1
SET c.state = $symbol
Strategies
There are at least two different ways to approach a problem like this:
- Brute force pattern matching
This is simply making your “AI” player look for certain patterns. For example, if you have an open-ended four in a row, it is probably a good idea to complete it to win the game.
This approach is ideal for Cypher, and it is actually quite a bit easier to do it in Cypher compared to a regular programming language like Java. - Heuristic searching
This would probably be the traditional approach to make an AI player for a game like Tic Tac Toe, Chess, or Kalaha. You recursively search all options you have and pick the path that leads to the best outcome, assuming your opponent would also make the best moves.
Recursive programming is, however, not ideal for Cypher… or at least so I thought (see later).
Pattern Matching
Cypher is really good at finding patterns, like a five in a row in a game like this. It is what it is designed for. Imagine doing the same in Java; you would need some clever, recursive algorithm to find matching cells in a row, something like this maybe:
private void findInARow(int length) { // length = 5 for five in a row
for (int y = 0; y < HEIGHT; y++) {
for (int x = 0; x < WIDTH; x++) {
if (board[x][y] != null) {
if (find(new Point(x,y), length, p -> {return new Point(p.x+1, p.y);})) {
System.out.println("Found " + board[x][y] + " horisontal starting at " + x + ", " + y);
return;
}
else if (find(new Point(x,y), length, p -> {return new Point(p.x+1, p.y+1);})) {
System.out.println("Found " + board[x][y] + " diagonal down right starting at " + x + ", " + y);
return;
}
else if (find(new Point(x,y), length, p -> {return new Point(p.x, p.y+1);})) {
System.out.println("Found " + board[x][y] + " vertical starting at " + x + ", " + y);
return;
}
else if (find(new Point(x,y), length, p -> {return new Point(p.x-1, p.y+1);})) {
System.out.println("Found " + board[x][y] + " diagonal down left starting at " + x + ", " + y);
return;
}
}
}
}
System.out.println("No five in a row found");
}
private boolean find(Point cell, int counter, Accumulator acc) {
if (counter == 1) {
return true;
}
Point nextCell = acc.accumulate(cell);
if (board[cell.x][cell.y] != board[nextCell.x][nextCell.y]) {
return false;
}
return find(nextCell, --counter, acc);
}
private interface Accumulator {
Point accumulate(Point p);
}
While in Cypher, the same things would be much simpler:
MATCH (c1)-[r1]->(c2)-[r2]->(c3)-[r3]->(c4)-[r4]->(c5)
WHERE c1.state IS NOT NULL AND c1.state = c2.state
AND c1.state = c3.state AND c1.state = c4.state AND c1.state = c5.state
AND r1.direction = r2.direction AND r1.direction = r3.direction
AND r1.direction = r4.direction
Well, it is much shorter than the Java version, but that is one long WHERE-clause. And the MATCH-clause is no joke either. Fortunately, there are ways to make it cleaner.
The simplest would be variable-length relationships where the same MATCH-clause could be expressed like this instead:
MATCH (c1)-[r*4]->(c2)
Much neater expression, right? The problem is that it makes the WHERE-clause even more monstrous. We still need to compare the directions of all those relationships, which we now do with r[0].direction = r[1].direction and so on.
But the nodes are harder to access. We only have the start node (c1) and end node (c2) of the path. To access the nodes in-between, we have to use startNode() and endNode() using the relationships. So the full expression becomes:
MATCH (c1)-[r*4]->(c2)
WHERE startNode(r[0]).state IS NOT NULL AND startNode(r[0]).state = endNode(r[0]).state AND startNode(r[0]).state = endNode(r[1]).state AND startNode(r[0]).state = endNode(r[2]).state AND startNode(r[0]).state = endNode(r[3]).state AND r[0].direction = r[1].direction AND r[0].direction = r[2].direction AND r[0].direction = r[3].direction
Hardly any better than the original one.
This is where we can make use of a new feature called Quantified Path Patterns (QPP), launched in Neo4j 5.9. Instead of just repeating a single relationship, we can repeat a full, intricate pattern. It also allows us to check things on individual nodes and relationships in that pattern.
One caveat is that in each pattern we only have access to the parts inside the current iteration, i.e., we cannot compare properties on an element in the current iteration of the pattern with a previous iteration.
One way to solve this is by doing an initial simple MATCH and then using that to compare the repeated pattern. Like this:
MATCH (c1)-[r1]->(c2)
WHERE c1.state IS NOT NULL AND c1.state = c2.state
WITH c2, r1
MATCH (c2)((c3 WHERE c3.state = c2.state)-[r WHERE r.direction = r1.direction]->(c4 WHERE c4.state = c2.state)){3}
We start by locating two adjacent nodes of the same state in the first MATCH.
In the second MATCH we declare the pattern we want to repeat (c3)-[r]->(c4) and we specify that we want it repeated exactly 3 times {3} (we already have the first repetition from the first MATCH).
Before this quantified path pattern, we see a reference to (c2) from the first MATCH. This tells it that the c2 node must match the first node in the quantified path pattern, i.e., the first instance of the c3 node. This way, we can compare all repetitions of the nodes with the state of the c2 node, and all repetitions of the relationships (r) with the direction of the r1 relationship from the first MATCH.
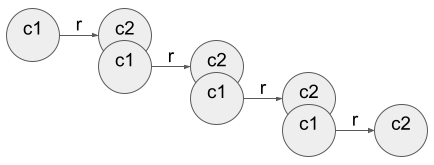
If we look at a simplified version of this MATCH where we remove all the WHERE’s:
MATCH (c2)((c3)-[r]->(c4)){3}
What we see here is that (c3)-[r]->(c4) should repeat 3 times. In the first iteration, c3 must be the same as c2 (the clause to the left). Every subsequent iteration c3 must be the same as the c4 from the iteration before. Just like we have the (c2) to specify how the path should start, there could also be something similar to specify how it must end, which would have come after the {3}, but we don’t need that here.
This solution isn’t very performant, though. The first MATCH will get a hit for every two adjacent cells on the board, which means that the second MATCH (with the QPP) will be performed that many times. The only reason we do the first match is to get something to compare the direction and state properties in the QPP with. In our case, we do, however, know that we only have four directions and two states, which means we can solve it like this as well:
UNWIND range(1,4) AS direction
UNWIND ["X","O"] AS state
MATCH ((c1 WHERE c1.state = state)-[r WHERE r.direction = direction]->
(c2 WHERE c2.state = state)){4}
Note that this time, the quantifier is {4} instead of {3}. Since we haven’t done the initial MATCH we need to repeat the QPP 4 times to find the full 5 in a row.
Now that we have those QPP basics down, we can start to put it to use to search for what we want.
I guess the first thing we would want our player to do is to see if there is anywhere we can put our mark that would complete a five in a row for us (and thus make us win).
UNWIND range(1,4) AS direction
MATCH p = ((()-[r WHERE r.direction = direction]->()){4})
WHERE size([n IN nodes(p) WHERE n.state = $symbol]) = 4
AND size([n IN nodes(p) WHERE n.state IS NULL]) = 1
WITH p LIMIT 1
FOREACH (n IN nodes(p) | SET n.state = $symbol)
Suppose we dive into what we make here. Just like before, we do the QPP, but we don’t check the state of the Cell nodes, just the direction of the relationships. Instead, we check the state afterward by counting how many nodes we found of different types. This is because we want to find a pattern with exactly one hole, but we don’t care where that hole is.
You might also have reacted to the fact that we set the state with a FOREACH. Shouldn’t we just set the state of one cell in our move? Yes, but since we know that all cells in the path are ours except one, we will, in the end, only change the state on one cell. This is just a convenient way to do it, instead of having to locate which is the empty cell.

If we can’t find that, we need to decide what to check next. In this path-finding approach to the AI, it is what we check for and in what order that defines how good our player will be. Things to check for are probably if the opponent can win and then block it, or if the opponent can create an open-ended four in a row, which we also need to block.
In the end, if we can’t find any of those patterns that we want to look for, we probably want to look for the longest sequence we have and continue that.
The longest path? There is a shortestPath() in Cypher, but no longestPath(). Well, that is easily solved. To find the longest sequence of cells with our symbol, we can simply do:
UNWIND range(1,4) AS direction
MATCH p = (((c1 WHERE c1.state = $symbol)
-[r WHERE r.direction = direction]
-(c2 WHERE c2.state = $symbol)){1,4})
WITH p ORDER BY length(p) DESC LIMIT 1
It follows the same pattern as our original QPP, but instead of repeating exactly 4 times, we repeat 1–4 times. Then, we order all our matches in descending length and pick the first 1 (which is the longest path).
But this isn’t really what we want. We want a cell to put our mark in that would build the longest path, whether that is on the end or in the middle. One two in a row could be better than another two in a row if it is connected to other of our cells, but missing one in the middle.
Here is a way to achieve that by doing two longest paths after one another. First, we look for all 5-cell sequences that have at least one of our marks and none from the other player, and then we pick the one with the most of our marks in it.
UNWIND range(1,4) AS direction
MATCH p = ((()-[r WHERE r.direction = direction]->()){4})
WITH p,
size([n IN nodes(p) WHERE n.state = $symbol]) as symbolCount,
size([n IN nodes(p) WHERE n.state IS NULL]) as nullCount
WHERE symbolCount > 0 AND nullCount = (5 - symbolCount)
WITH p
ORDER BY symbolCount DESC LIMIT 1
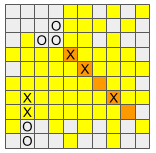
That gives us the five-cell sequence where we want to place our mark. But now we need to know where in that sequence to place it. We do that by looking for a cell (c1) that is part of that sequence, and that is empty, and that has the longest trail of our marks connected:
MATCH p2 = ((c1 WHERE c1.state IS NULL AND c1 IN nodes(p))- -()
((c2 WHERE c2.state = $symbol AND c2 IN nodes(p))
- -(c3 WHERE c3.state = $symbol AND c3 IN nodes(p)))*)
WITH p2 ORDER BY length(p2) DESC LIMIT 1
WITH HEAD(nodes(p2)) AS n
SET n.state = $symbol
So now we have all those checks we want to do in a sequence, and we only want to do the next step if we haven’t had a match on the previous one. First, we want to check if we can win with one mark, then if we should block the opponent, and so on.
One way to achieve this is to do each of these parts in a CALL-subquery, return the number of cells altered and only do the next step if that is 0.
// Start by checking if there is anywhere where we can put our mark and win directly
CALL {
UNWIND range(1,4) AS direction
MATCH p = ((()-[r WHERE r.direction = direction]->()){4})
WHERE size([n IN nodes(p) WHERE n.state = $symbol]) = 4 AND size([n IN nodes(p) WHERE n.state IS NULL]) = 1
WITH p LIMIT 1
FOREACH (n IN nodes(p) | SET n.state = $symbol)
RETURN count(p) AS updated1
}
// If the opponent can win next round with one mark, block it
CALL {
WITH updated1
WITH *
WHERE updated1 < 1
UNWIND range(1,4) AS direction
MATCH p = ((()-[r WHERE r.direction = direction]->()){4})
WHERE size([n IN nodes(p) WHERE n.state = $symbol]) = 0 AND size([n IN nodes(p) WHERE n.state IS NULL]) = 1
WITH p ORDER BY length(p) DESC LIMIT 1
FOREACH (n IN [x IN nodes(p) WHERE x.state IS NULL] | SET n.state = $symbol)
RETURN count(p) AS updated2
}
// ... and so on...
The approach described here is, of course, just one way to do this.
Looking at the different implementations submitted to the challenge, there were many others. The winning team had a similar pattern-matching approach but implemented in a very different way.
You can see that at the end of the post.
Heuristic Searching
Heuristic searching, or the Negamax algorithm, is the traditional way to implement an AI player for a board game. You recursively test all possible moves you can do, followed by all possible opponent moves, and so on. The “heuristic” part of it is that, unless it is a small 3*3 Tic Tac Toe game, you will not be able to search all the way to the end. Instead you need to have a way to heuristically determine how good a certain game state is (the quality of this defines how good the AI player becomes).

Doing recursive programming is, however, not possible in Cypher, so this is not a feasible approach for a Cypher Tic Tac Toe player…
Or at least so I thought…
Along came Satia Herfert from the Neo4j Engineering team Cypher Planner, who did just that.
I won’t give the full details on how Satia did this, nor will I share his full Cypher query; it is too long. That is a topic for a blog post on its own. However, I will give an overview of how Satia approached the task of a recursive algorithm in Cypher.
Before going into this section, I just wanted to say thank you to Satia for letting me use his Cypher examples here. And, of course, also for figuring out how to pull off such a feat in Cypher.
To do this recursive Negamax algorithm in Cypher, you need three things:
- A way to determine all possible moves given a game state
- A heuristic algorithm to determine the “score” for a certain game state
- A mechanism for the recursiveness
Determining possible moves is as simple as listing all empty cells. Well, to speed up the algorithm, it is good to limit at a bit, so let’s list all empty cells that have a non-empty neighbor (unless the board is empty).
WITH *, NOT EXISTS { (c2:Cell) WHERE c2.state IS NOT NULL } AS fieldEmpty
MATCH (possibleMove:Cell)
WHERE possibleMove.state IS NULL
AND (fieldEmpty OR
EXISTS { (possibleMove)- -(neighbor) WHERE neighbor.state IS NOT NULL})
To generate the score for a position, Satia looked for all 5-cell sequences and gave a positive score for those only containing our symbol, and a negative for those containing our opponent’s.
MATCH line = (:Cell)-[r1]->()-[r2]->()-[r3]->()-[r4]->()
WHERE r2.direction = r1.direction
AND r3.direction = r1.direction
AND r4.direction = r1.direction
CALL {
// All lines that only contain my symbol generate points for me.
// More symbols - exponentially more points.
WITH *
WITH * WHERE all(n IN nodes(line) WHERE n.state = $symbol OR n.state IS NULL)
UNWIND nodes(line) AS node
WITH * WHERE node.state = $symbol
WITH count(*) AS myCells WHERE myCells > 0
RETURN CASE myCells WHEN 5 THEN 100_000 ELSE toInteger(10 ^ (myCells - 1)) END AS points
UNION ALL
// All lines that only contain the other symbol generate points against me.
WITH *
WITH * WHERE all(n IN nodes(line) WHERE n.state = OTHER OR n.state IS NULL)
UNWIND nodes(line) AS node
WITH * WHERE node.state = OTHER
WITH count(*) AS otherCells WHERE otherCells > 0
RETURN -1 * CASE otherCells WHEN 5 THEN 100_000 ELSE toInteger(10 ^ (otherCells - 1)) END AS points
}
RETURN sum(points) AS score
And now to the tricky part, the recursiveness. What is a recursive function call? It is the CPU using the stack to keep track of the state so that it can be rolled back. You can’t do recursive calls in Cypher directly, but you can implement a stack. In fact, you have the world’s best database at your disposal to manage that stack, and that is what Satia did.
What is important to remember is that you don’t need to put the entire game state on the stack. You just need to put what is needed to roll back a move. Satia defined a number of commands, represented by integers, each with a number of integer parameters, to put on the stack. So, each stack entry is a list of integers, where the first defines the command.
WITH 0 AS REC // -- format [REC, depth, turn] ; depth >= 0 and turn IN [1,-1]; 1 means this player, -1 means other player
, 1 AS DO_MOVE // -- format [DO_MOVE, row, col, turn]
, 2 AS UNDO_MOVE // -- format [UNDO_MOVE, row, col]
, 3 AS NEGATE_SCORE // -- format [NEGATE_SCORE, depth, row, col]
, 4 AS SCORE // -- format [SCORE, score, depth, row, col]
, 5 AS MAXIMIZE_SCORES // -- format [MAXIMIZE_SCORES, depth]
, CASE $symbol WHEN 'X' THEN 'O' ELSE 'X' END AS OTHER
To create the stack and push the first command, you do:
CREATE (stack:Stack:Head {value: [REC, 0, 1]})
There are no for-loops in Cypher, but that can be solved like this (hoping that 100,000 iterations are enough):
UNWIND range(1, 100_000) as step
CALL {
WITH *
…
}
Pop a command from the stack with:
MATCH (commandNode:Head)
WITH *, commandNode.value AS command
OPTIONAL MATCH (commandNode)- ->(nextHead)
SET nextHead:Head
DETACH DELETE commandNode
Executing the commands would be done like this:
CALL {
WITH *
WITH * WHERE head(command) = REC
WITH *
, command[1] AS depth
, command[2] AS turn
…
UNION ALL
WITH *
WITH * WHERE head(command) = DO_MOVE
WITH *
, command[1] AS row
, command[2] AS col
, command[3] AS turn
…
UNION ALL
…<continues analogous>
}
Finally, you need a part that, for every possible move (from the first routine in this section), does the “recursive call” (i.e., putting the proper commands on the stack).
CALL {
WITH *
WITH *, possibleMove.row AS row, possibleMove.column AS col
MATCH (head:Head)
REMOVE head:Head
CREATE (:Head:Stack {value: [DO_MOVE, row, col, turn]})-[:NEXT]->
(:Stack {value: [REC, depth + 1, -1 * turn]})-[:NEXT]->
(:Stack {value: [NEGATE_SCORE, depth, row, col]})-[:NEXT]->
(:Stack {value: [UNDO_MOVE, row, col]})-[:NEXT]->
(head)
}
Oh, one more thing. We need to hide from the game that we were naughty and borrowed the database for our stack implementation. So the routine ends with this, and once our move is done, no one can see that we did anything more than putting an “X” or an “O” in one of the cells.
MATCH (del:Head|Stack|Result)
DETACH DELETE del
That’s it. Turns out you can do “recursive” calls in Cypher. We just touched the surface of everything Satia did, though. As I said, all details would require a blog post of its own. But hopefully, you got an idea of how he approached the Negamax algorithm in Cypher.
What About the Game?
This is all nice with different algorithms and Cypher statements. But who won the game?
Was it Satia with his Heuristic player? No, but it was actually a team from the same Engineering team that won. The winners were Gustav Hedengran and Lars Korduner.

What was the winning strategy then? Well, it is hard to know why one player wins over another, but I believe I know what differs in this implementation from all the others.
Most implementations, like the one described above, aim to build as long straight paths as possible and block the same for the opponent. They specifically know that if the opponent has three in a row, it needs to be blocked immediately.
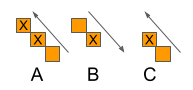
They do, however, not consider the most powerful construct in five-in-a-row, the Fork. The winning team did just that.
A fork is where you can, with a single mark, build three in a row in two directions at once, and thus, the opponent can’t block both of them. After one is blocked, you can make an open-ended four in a row of the other one, and then, once one end is blocked, you make the five in a row and win.
I bet you want to see the full Cypher query used by the winning team to make the player moves. Sure, here you go, but don’t expect me to explain what it does… because… eh… I don’t want to 😉
CALL {
CALL {
UNWIND range(1,4) AS direction
MATCH p = (start:Cell)(()-[r WHERE r.direction = direction]->()){4}(end)
OPTIONAL MATCH (before_start)-[r0]->(start)
WHERE r0.direction = direction
OPTIONAL MATCH (end)-[r5]->(after_end)
WHERE r5.direction = direction
RETURN p, before_start, start, end, after_end, direction
} // -- all valid paths
WITH *
WHERE all(node IN nodes(p) WHERE node.state IS NULL OR node.state = $symbol) OR
all(node IN nodes(p) WHERE node.state IS NULL OR node.state <> $symbol) // -- exclude all paths that include both symbols since they cannot lead to victory
WITH *,
CASE
WHEN before_start IS NOT NULL AND before_start.state IS NULL AND end.state IS NULL THEN 1
WHEN start.state IS NULL AND after_end IS NOT NULL AND after_end.state IS NULL THEN 2
ELSE 0
END AS openEnded
WITH *,
size([node IN nodes(p) WHERE node.state = $symbol]) AS myScore,
size([node IN nodes(p) WHERE node.state <> $symbol]) AS otherScore
// -- the two size filters above are enough, since any path including both symbols have already been excluded above
UNWIND nodes(p) AS candidate
WITH * WHERE candidate.state IS NULL
WITH *,
CASE
WHEN myScore = 4 THEN 2
WHEN otherScore = 4 THEN 1
ELSE 0
END AS isWinningMove, // -- 2 means it is my win, 1 means that opponent could win in next move
CASE
WHEN myScore = 3 AND ((openEnded = 1 AND candidate <> end) OR (openEnded = 2 AND candidate <> start)) THEN 2
WHEN otherScore = 3 AND ((openEnded = 1 AND candidate <> end) OR (openEnded = 2 AND candidate <> start)) THEN 1
ELSE 0
END AS isThreeWinningMove,
CASE
WHEN myScore = 3 THEN 1
ELSE 0
END AS isMyThreeMove,
CASE
WHEN otherScore = 3 THEN 1
ELSE 0
END AS isOtherThreeMove,
CASE
WHEN myScore = 2 AND ((openEnded = 1 AND candidate <> end) OR (openEnded = 2 AND candidate <> start)) THEN 1
ELSE 0
END AS isMyTwoMove,
CASE
WHEN otherScore = 2 AND ((openEnded = 1 AND candidate <> end) OR (openEnded = 2 AND candidate <> start)) THEN 1
ELSE 0
END AS isOtherTwoMove
WITH candidate,
direction,
max(isWinningMove) AS maxIsWinningMove,
max(isThreeWinningMove) AS maxIsThreeWinningMove,
max(isMyThreeMove) AS maxIsMyThreeMove,
max(isOtherThreeMove) AS maxIsOtherThreeMove,
max(isMyTwoMove) AS maxIsMyTwoMove,
max(isOtherTwoMove) AS maxIsOtherTwoMove,
sum((myScore + otherScore + toInteger(openEnded > 0))) AS candidateScore // -- give an additional point for open-ended paths, as a heuristic
WITH candidate,
sum(maxIsWinningMove) AS isWinningMove,
sum(maxIsThreeWinningMove) AS isThreeWinningMove,
sum(maxIsMyThreeMove) AS isMyThreeMoveSum,
sum(maxIsOtherThreeMove) AS isOtherThreeMoveSum,
sum(maxIsMyTwoMove) AS isMyTwoMoveSum,
sum(maxIsOtherTwoMove) AS isOtherTwoMoveSum,
sum(candidateScore) + count(*) AS score // -- give one point extra for each direction that a candidate advances play in, as a heuristic
WITH *,
CASE
WHEN isMyThreeMoveSum >= 2 THEN 2
WHEN isOtherThreeMoveSum >= 2 THEN 1
WHEN isMyThreeMoveSum > 0 AND isMyTwoMoveSum > 0 THEN 2
WHEN isOtherThreeMoveSum > 0 AND isOtherTwoMoveSum > 0 THEN 1
WHEN isMyTwoMoveSum >= 2 THEN 2
WHEN isOtherTwoMoveSum >= 2 THEN 1
ELSE 0
END AS isFork
WITH * ORDER BY isWinningMove DESC, isThreeWinningMove DESC, isFork DESC, score DESC
LIMIT 1
RETURN candidate, isWinningMove
UNION
// -- When the game will for sure end in a tie we still need to update the game
MATCH (candidate) WHERE candidate.state IS NULL
RETURN candidate, -1 AS isWinningMove LIMIT 1
}
WITH * ORDER BY isWinningMove DESC
LIMIT 1
SET candidate.state = $symbol
I hope you enjoyed our journey into the world of solving board games with graph queries and learned a bit, as I did.
Thanks to all the participants in the competition, this was a lot of fun.
If you want to learn more about Cypher, check out the Cypher section of our GraphAcademy.
Free, Self-Paced, Hands-on Online Training
Other Articles
This post has discussed the topic of Quantified Path Patterns. Here are two other articles about that subject:
- Getting From Denmark Hill to Gatwick Airport With Quantified Path Patterns
- Did You Take the Neo4j 5 Cypher Bullet Train?
And, of course, the documentation
Tic Tac Toe Challenge in Cypher was originally published in Neo4j Developer Blog on Medium, where people are continuing the conversation by highlighting and responding to this story.