Tutorial: Applied Graph Embeddings

Goals

This guide provides a hands on walk through of the node2Vec graph embedding algorithm in the Neo4j Data Science Library.

Prerequisites

Please have Neo4j (version 4.0 or later) and Graph Data Science Library (version 2.0 or later) downloaded and installed to use graph embeddings. You will also need to have Python installed to follow the second half of this guide.

Intermediate

Graph embeddings were introduced in version 1.3 of the Graph Data Science Library (GDSL). They can be used to create a fixed size vector representation for nodes in a graph. In this guide we’ll learn how to use these algorithms to generate embeddings and how to interpret them using visualization techniques.

The code examples used in this guide can be found in the neo4j-examples/applied-graph-embeddings GitHub repository. For background reading about graph embeddings, see the Graph Embeddings Developer Guide.

European Roads dataset

We’re going to use a dataset of European Roads compiled by Lasse Westh-Nielsen and described in more detail in his blog post. The dataset contains 894 towns, 39 countries, and 1,250 roads connecting them.

To import the dataset, run the following:

CREATE CONSTRAINT places IF NOT EXISTS ON (p:Place) ASSERT p.name IS UNIQUE;
CREATE CONSTRAINT countries IF NOT EXISTS ON (c:Country) ASSERT c.code IS UNIQUE;

LOAD CSV WITH HEADERS FROM "https://github.com/neo4j-examples/graph-embeddings/raw/main/data/roads.csv"
AS row

MERGE (origin:Place {name: row.origin_reference_place})
SET origin.countryCode = row.origin_country_code

MERGE (destination:Place {name: row.destination_reference_place})
SET destination.countryCode = row.destination_country_code

MERGE (c_origin:Country {code: row.origin_country_code})

MERGE (c_destination:Country {code: row.destination_country_code})

MERGE (origin)-[eroad:EROAD {number: row.road_number}]->(destination)
SET eroad.distance = toInteger(row.distance), eroad.watercrossing = row.watercrossing

MERGE (origin)-[:IN_COUNTRY]->(c_origin)
MERGE (destination)-[:IN_COUNTRY]->(c_destination);

We can see the schema in the diagram below:

Figure 1. European Roads Graph Schema

This diagram was generated by running CALL db.schema.visualization() in the Neo4j Browser after importing the data.

In the next section we’re going to run graph embeddings over the towns and roads to generate a vector representation for each town.

Running graph embeddings

We’re going to use the FastRP algorithm, which is one of 3 embedding algorithms available in the Graph Data Science Library. FastRP creates embeddings based on random walks of a node’s neighborhood. For more information on the inner workings of FastRP, see this blog post.

We’re going to first run the streaming version of this procedure, which returns a stream of node IDs and embeddings. The algorithm only requires one mandatory configuration parameter, embeddingDimension, which is the size of the vector/list of numbers to create for each node. Additionally, there a many optional parameters that can be used to further tune the resulting embeddings, which are described in detail in the API documentation.

In order to create our embeddings, we must first create a graph projection:

CALL gds.graph.project(
  'places_undir',
  'Place',
  {EROAD: {orientation: 'UNDIRECTED'}}
)

In relationshipProjection, we specify orientation: "UNDIRECTED" so that the direction of the EROAD relationship type is ignored on the projected graph that the algorithm runs against. This is because FastRP uses a random walk approach, so by using an undirected graph we are allowing the random walk to traverse the relationship in both directions.

We can run the algorithm with the following query:

CALL gds.fastRP.stream('places_undir',
  {
    embeddingDimension: 10
  }
)
YIELD nodeId, embedding
RETURN gds.util.asNode(nodeId).name AS place, embedding
LIMIT 5

If we run the query, it will return the following output:

Table 1. Results
place	embedding
"Larne"	[0.5786177515983582,-0.4012638330459595,-0.16752511262893677,-0.7087218761444092, 0.37056204676628113,-0.9627646803855896,-0.17660734057426453, 0.5529423356056213, -0.1881837546825409, 0.20178654789924622]
"Belfast"	[0.5153923034667969, -0.22510990500450134, -0.199273020029068, -0.6573874354362488, 0.2203015387058258, -1.0398733615875244, -0.19496142864227295, 0.49318426847457886, -0.024694180116057396, 0.08109953254461288]
"Dublin"	[0.19724464416503906, -0.21975931525230408, 0.019983142614364624, -0.5070462822914124, 0.13303154706954956, -0.8911266326904297, -0.278847873210907, 0.6584466695785522, -0.21137264370918274, -0.22576412558555603]
"Wexford"	[0.2206020951271057, -0.21055060625076294, 0.24700090289115906, -0.7486459016799927, 0.1806430220603943, -0.47783035039901733, -0.3107770085334778, 0.4667920470237732, -0.27482911944389343, -0.6629651784896851]
"Rosslare"	[0.24542507529258728, -0.18245811760425568, 0.33527031540870667, -0.8160518407821655, 0.19655174016952515, -0.33142057061195374, -0.2781609892845154, 0.2243683785200119, -0.3783305585384369, -0.8914577960968018]

This procedure is non deterministic, so we’ll get different results each time that we run it.

Everything looks fine so far, we’ve been successful in returning embeddings for each node.

Further exploration will be easier if we store the embeddings in Neo4j, so we’re going to do that using the write version of the procedure. We can store the embeddings by running the following query:

CALL gds.fastRP.write(
  'places_undir',
  {
    embeddingDimension: 256,
    writeProperty: 'embedding'
  }
);

Table 2. Results of gds.fastRP.write()
nodeCount	nodePropertiesWritten
preProcessingMillis	computeMillis
writeMillis	configuration
894	894
0	8
99	{"writeConcurrency":4,"nodeSelfInfluence":0,"relationshipWeightProperty":null,"propertyRatio":0.0,"concurrency":4,"normalizationStrength":0.0,"writeProperty":"embedding","iterationWeights":[0.0,1.0,1.0],"embeddingDimension":256,"nodeLabels":[""],"sudo":false,"relationshipTypes":[""],"featureProperties":[],"username":null}

In the next section we’re going to explore these graph embeddings using visualization techniques.

Visualizing graph embeddings

We’re now going to explore the graph embeddings using the Python programming language, the Neo4j Python driver, and some popular Data Science libraries. We’ll create a scatterplot of the embedding and we want to see whether it’s possible to work out which town a country belongs to by looking at its embedding.

The code examples used in this section are available in Jupyter notebook form in the project repository. In this notebook you will find the code to import the relevant packages and make the connection to the Neo4j database. In particular, you will require the Python packages neo4j, pandas, sklearn, and altair, which are pip installable.

We’re going to use the driver to execute a Cypher query that returns the embedding for towns in the most popular countries, which are Spain, Great Britain, France, Turkey, Italy, Germany, and Greece. Restricting the number of countries will make it easier to detect any patterns once we start visualizing the data. Once the query has run, we’ll convert the results into a Pandas data frame:

query = '''MATCH (p:Place)-[:IN_COUNTRY]->(country)
           WHERE country.code IN ["E", "GB", "F", "TR", "I", "D", "GR"]
           RETURN p.name AS place, p.embedding AS embedding, country.code AS country
'''

df = pd.DataFrame([dict(_) for _ in conn.query(query)])
df.head()

Now we’re ready to start analyzing the data.

At the moment our embeddings are of size 256, but we need them to be of size 2 so that we can visualize them in 2 dimensions. The t-SNE algorithm is a dimensionality reduction technique that reduces high dimensionality objects to 2 or 3 dimensions so that they can be better visualized. We’re going to use it to create x and y coordinates for each embedding.

The following code snippet applies t-SNE to the embeddings and then creates a data frame containing each place, its country, as well as x and y coordinates.

X_embedded = TSNE(n_components=2, random_state=6).fit_transform(list(df.embedding))

places = df.place
tsne_df = pd.DataFrame(data = {
    "place": places,
    "country": df.country,
    "x": [value[0] for value in X_embedded],
    "y": [value[1] for value in X_embedded]
})
tsne_df.head()

The content of the data frame looks as follows:

Table 3. Results
place	country	x	y
Larne	GB	23.597162	-3.478853
Belfast	GB	23.132071	-4.331254
La Coruña	E	-6.959006	7.212301
Pontevedra	E	-6.563524	7.505499
Huelva	E	-11.583806	11.094340

Since this is not a deterministic embedding, your results will vary from the above.

We can run the following code to create a scatterplot of our embeddings:

alt.Chart(tsne_df).mark_circle(size=60).encode(
    x='x',
    y='y',
    color='country',
    tooltip=['place', 'country']
).properties(width=700, height=400)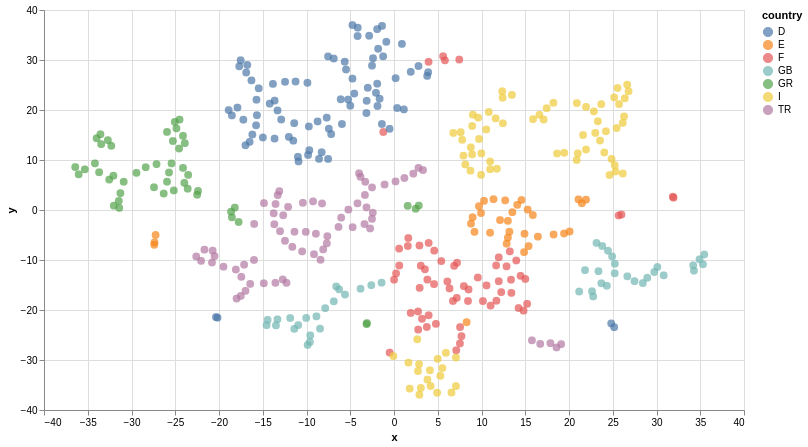

From a quick visual inspection of this chart we can see that the embeddings seem to have clustered by country.

Next Steps

Visualizing embeddings are often only an intermediate step in our analysis.

Cluster nodes based on the similarity of their embeddings using a k-means clustering algorithm
Predict the country of town by using a nearest neighbors algorithm that takes embeddings as input
Use the embeddings as features for a machine learning algorithm

Resources

Was this page helpful?